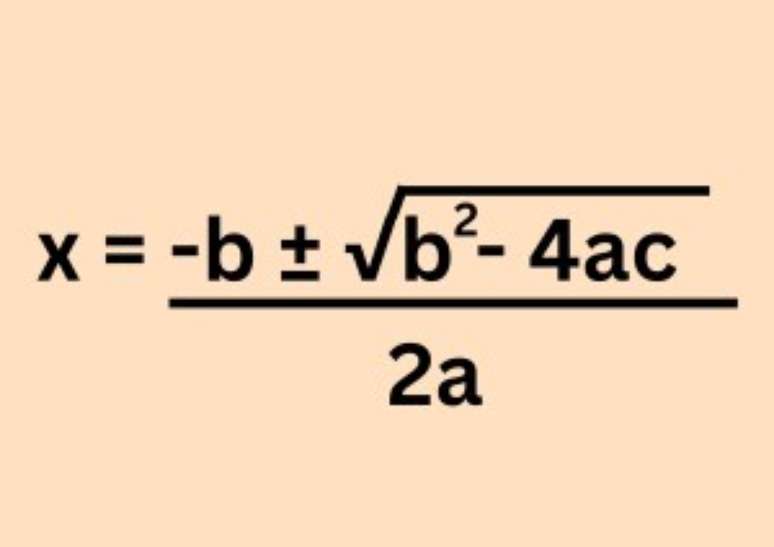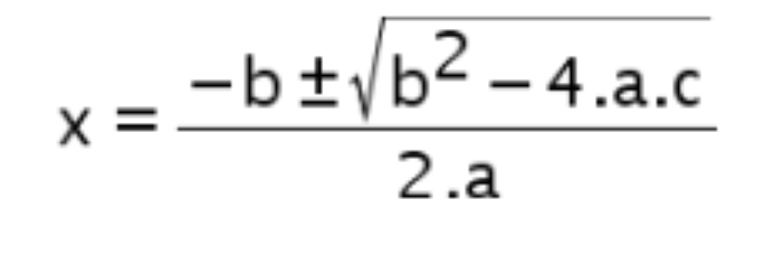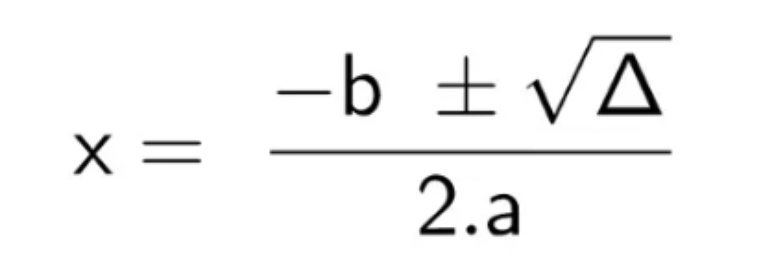O que é a fórmula de Bhaskara e como resolve-la
Saiba mais sobre a fórmula de Bhaskara, sua utilidade e como usar esse método em equações de segundo grau.
A fórmula de Bhaskara é usada para encontrar as raízes de equações de segundo grau e é importante em provas e concursos. Seu cálculo envolve o discriminante (delta) e fórmulas para obter os valores de X1 e X2.
A fórmula de Bhaskara é importante para a resolução de equações de segundo grau. Porém, ela nem sempre é lembrada e, diante de questões de matemática em provas e concursos, essa falta de memória pode custar alguns pontos do resultado final.
Por isso, é essencial ter em mente qual é e como funciona a fórmula de Bhaskara, já que questões de equação de segundo grau podem estar presentes em provas importantes, como o Enem e a Fuvest.
O que é a fórmula de Bhaskara?
A fórmula de Bhaskara é um método usado para determinar quais são as raízes de uma equação de segundo grau, também chamada de equação quadrática, representada pelo cálculo a seguir: ax² + bx + c = 0.
Com a fórmula de Bhaskara, é possível seguir um passo a passo para resolver equações, já que ela ajuda a definir os valores de X que geram resultado zero em uma equação. Isso facilita a resolução da questão.
O nome da fórmula, usado só no Brasil, é inspirado no indiano Bhaskara Akaria (1114 - 1185), que era matemático, astrólogo e astrônomo. A origem do uso do nome na fórmula no Brasil é incerta e começou na década de 1960.
Para que serve a fórmula de Bhaskara?
A fórmula de Bhaskara serve para resolver equações de segundo grau, encontrando as raízes reais da equação a partir dos coeficientes (números que multiplicam X, também chamado de incógnita).
Vale lembrar que a equação de segundo grau, em sua versão normal ou reduzida, é representada pela seguinte escrita: ax² + bx + c = 0. Neste caso, os coeficientes são os números que substituem as letras a, b e c.
Já a fórmula de Bhaskara está representada a seguir:
Dessa maneira, o objetivo é descobrir o valor de X, ou seja, a raiz da equação. As letras representam os números reais presentes em uma equação.
Para melhorar a compreensão, a fórmula de Bhaskara é dividida entre a etapa com a fórmula do discriminante (que está dentro da raiz quadrada, também representada pela letra grega delta) e a fórmula de Bhaskara em si.
Com isso, outra representação é:
Como resolver a fórmula de Bhaskara?
O primeiro passo para resolver equações com a fórmula de Bhaskara é calcular o valor do discriminante, ou seja, resolver as operações dentro da raiz quadrada, representadas pela letra delta. Ao realizar o cálculo, o discriminante traz três possibilidades:
- Quando o delta é menor do que zero, significa que a equação não tem resultados reais;
- Caso o delta seja igual a zero, significa que a equação possui um resultado real ou dois resultados iguais;
- Quando o delta for maior do que zero, quer dizer que a equação possui dois resultados diferentes.
Após calcular o valor de delta, o próximo passo é inserir o resultado e os coeficientes da equação de segundo grau na fórmula de Bhaskara. Para isso, basta substituir as letras a, b e c pelos números informados na equação.
Em seguida, é necessário realizar as operações matemáticas inseridas na fórmula. No caso do Bhaskara, o sinal de mais e menos mostra que dois cálculos devem ser feitos:
- Cálculo para localizar a raiz que tenha resultado positivo;
- Cálculo que indica que a raiz tem resultado negativo.
Por isso, os resultados da fórmula são indicados como X1 e X2.
Um exemplo de uso da fórmula de Bhaskara pode ser visto a partir da seguinte equação do segundo grau: x2 + 8x – 9 = 0
Nesse caso, os coeficientes são: a = 1, b = 8, c = – 9.
O delta, no exemplo,teria o cálculo a seguir:
Δ = b2 – 4ac
Δ = 82 – 4·1·(– 9)
Δ = 64 + 36
Δ = 100
Substituindo esses valores na fórmula de Bhaskara, obtemos o cálculo abaixo:
x = – b ± √Δ
2a
x = – 8 ± √100
2·1
x = – 8 ± 10
2
x' = – 8 + 10
2
x' = 2
2
x' = 1
x'' = – 8 – 10
2
x'' = – 18
2
x'' = – 9
Dessa maneira, após o uso da fórmula de Bhaskara na equação de segundo grau, o resultado alcançado são duas raízes: x1 = 1 e x2' = – 9
Saiba mais dicas para memorizar fórmulas e impulsionar os seus estudos para vestibulares, provas e concursos diversos. Navegue pelos conteúdos do Terra Educar!